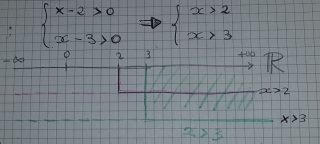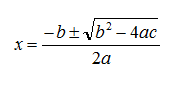EQUAZIONI LOGARITMICHE

EQUAZIONI LOGARITMICHE

Dopo aver definito i logaritmi, capito a che cosa servono e scoperto le loro proprietà, oggi finalmente passiamo a parlare di argomenti “seri”. Caro nipote, preparati: le equazioni logaritmiche!

PER SAPERNE DI PIÙ:

• NIPOTINI E LOGARITMI 
• A CHE SERVONO I LOGARITMI ???
• PROPRIETÀ DEI LOGARITMI

EQUAZIONI LOGARITMICHE : che cosa sono

Si dicono logaritmiche quelle equazioni in cui l’incognita compare all’argomento di uno o più logaritmi.

EQUAZIONI LOGARITMICHE. Come risolverle

Per risolvere le equazioni logaritmiche, dobbiamo cercare di ottenere un solo logaritmo sia prima che dopo il segno di uguale, in modo da poter ricondurre l’equazione logaritmica ad un’equazione negli argomenti dei logaritmi.

Ovviamente deve sempre essere l’argomento del logaritmo maggiore di zero.

In pratica:

1. imposta un sistema ponendo tutti gli argomenti dei logaritmi maggiori di zero per determinare il CAMPO DI ESISTENZA C.E.
2. risolvi il sistema di disequazioni impostato, trovando l’intervallo in cui le soluzioni dell’equazione logaritmica sono accettabili
3. determina le soluzioni dell’equazione logaritmica
4. verifica che le soluzioni appartengano all’intervallo di validità

EQUAZIONI LOGARITMICHE. Esempi di risoluzione

ESEMPIO 1

Si consideri l’equazione logaritmica

log (x-2) – log (x-3) = log 4

Devo imporre che tutti gli argomenti dei logaritmi siano maggiori di 0

• x-2 > 0
• x – 3 > 0

Risolvendo otteniamo

• x>2
• x > 3

Ovvero 3 < x < +∞ x ∈ (3; +∞)

Adesso dobbiamo risolvere l’equazione assegnata.

log (x-2) – log (x-3) = log 4

Applicando il teorema del quoziente, possiamo scrivere:

log ((x-2) / (x-3)) = log 4

Uguagliando gli argomenti :

(x-2) / (x-3) = 4 ⇒ x-2 = 4 (x-3)

da cui, risolvendo rispetto ad x, otteniamo :

x = 10/3

Ora ci resta solo da verificare se le soluzioni appartengono all’intervallo di validità:

x = 10/3 ∈ (3; +∞)

ovvero : la soluzione è accettabile

Riassumendo:

Facciamo ancora un altro esempio

ESEMPIO 2

Si consideri l’equazione logaritmica

log ₂ (x + 1) = log ₄ (2x + 5)

Innanzitutto devo operare un cambiamento di base:

log ₂ (x + 1) = log ₂ (2x + 5) / log ₂ (4)

Siccome 4 = 2² e log ₂ 2² = 2 log ₂ 2 = 2

Abbiamo

log ₂ (x + 1) = log ₂ (2x + 5) / 2

Devo imporre che tutti gli argomenti dei logaritmi siano maggiori di 0

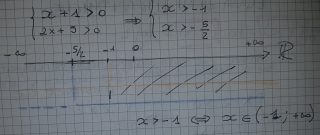
• x + 1 > 0
• 2 x + 5 > 0

Risolvendo otteniamo

• x > – 1
• x > – 5/2

Ovvero -1 < x < +∞ x ∈ (-1 ; +∞)

Dobbiamo ora risolvere l’equazione logaritmica ottenuta:

log ₂ (x + 1) = log ₂ (2x + 5) / 2

Ricordando la proprietà della potenza di un logaritmo

log _a y ^m = m * log _a y

L’equazione logaritmica diventa

log ₂ (x + 1) = log ₂ (2x + 5)^1/2

Uguagliando gli argomenti dei logaritmi otteniamo

(x + 1) = (2x + 5)^1/2  

ovvero :

(x + 1) = √(2x + 5)

Eliminiamo la radice quadrata, elevando entrambi i membri dell’equazione al quadrato. Otteniamo :

(x + 1)² = (2 x + 5)

Ricordando le regole per il calcolo dei prodotti notevoli ((a+ b)² = a² + 2ab + b² ), otteniamo:

x² + 2x + 1 = 2x + 5

⇔  x² + 2x + 1 – 2x – 5 = 0

Semplificando, abbiamo

x²  – 4 = 0

che è la differenza di due quadrati. Abbiamo quindi:

(x-2) (x+2) = 0

Che ha come soluzioni:

x₁ = -2 ; x₂ = 2

Dobbiamo ora verificare che le soluzioni appartengano a ll’intervallo di validità : x ∈ (1; +∞)?

x₁ = -2 non è inclusa nell’intervallo determinato, per cui l’unica soluzione accettabile è

x₂ = 2

Passiamo ora a risolvere un’equazione logaritmica di secondo grado.

Ricordiamo che

(Log x)² = Log² x

Questa scrittura si legge Logaritmo al quadrato di x e significa
(Log x)·(Log x)

Invece Log x² significa Log (x·x)  ed indica il Logaritmo di x al quadrato

ESEMPIO 3

Proviamo a risolvere insieme l’equazione seguente:

(Log x²)² – 2 Log x³ + 2 = 0

Applicando il teorema del logaritmo di una potenza, possiamo scrivere

2(Log x)² – 2 * 3Log x + 2 = 0

Determiniamo il C.E. del logaritmo, che è definito solo se l’argomento è maggiore di zero. In questo caso abbiamo solo la condizione

x > 0

Per risolvere quest’equazione di secondo grado, operiamo una sostituzione, ponendo

Log x = t

L’equazione logaritmica assegnata diventa

4t² – 6t + 2 = 0

Dividendo tutto per 2 abbiamo

2t² – 3t + 1 = 0

Applichiamo ora la formula risolutiva delle equazioni di secondo grado:

Che in questo caso mi dà

t_{1,2 =} [ 3± √9 – 4(2)(1)] / 4

Le soluzioni sono quindi:

t _1,2 =( 3± 1) / 4

ovvero:

• t ₁ = 1
• t ₂ = 1 / 2

Dobbiamo ora andare a sostituire i valori ottenuti nella posizione fatta.

Otteniamo due equazioni

• log x = t ₁  ovvero  log x = 1
• log x  = t ₂  ovvero  log x = 1 / 2

Risolviamo la prima. Ricordando che se non è specificata nessuna base, si intende che il log è in base 10, per la definizione di logaritmo abbiamo

x = 10¹ = 10 > 0 ACCETTABILE

Possiamo anche dire che, siccome 1 = log 10, abbiamo

log x = log 10

da cui,  eguagliando gli argomenti, otteniamo la soluzione

x = 10 accettabile

La seconda equazione ci dà

log x = 1 / 2

Moltiplicando tutto per 2 abbiamo

2 log x = 1

Ovvero, per le proprietà dei log

log x² = log 10

Uguagliando gli argomenti, otteniamo

x² = 10

che ha due soluzioni

• x₁ = – √10 < 0 e quindi NON ACCETTABILE
• x₂ =  √10 > 0 ACCETTABILE

In conclusione: l’equazione data ha due soluzioni :

• x = 10
• x =  √10

ESEMPIO 4.

Facciamo un altro esempio con le equazioni logaritmiche di secondo grado.

Complichiamoci un pochino i calcoli e proviamo a risolvere un’equazione logaritmica frazionaria.

Consideriamo la seguente equazione

14 / (log ₅ x + 2) +  4 / (log ₅ x -1) = 3

Imponiamo che i denominatori siano ≠0 e che l’argomento del log sia maggiore di zero

Otteniamo

• log ₅ x + 2 ≠0
• log ₅ x -1≠0
• x>0

Risolvendo ricaviamo:

• log ₅ x ≠-2   x ≠ 5 ^-2≠ 1/25
• log ₅ x ≠1 x ≠ 5
• x>0

Il C.E. è quindi x∈R⁺, x≠1/25 ∧ x ≠ 5

Per semplificare le scritture, imponiamo che sia

log ₅ x = t

L’equazione data diventa:

14/ (t + 2) + 4 / (t – 1) = 3

Calcolando il minimo comune denominatore abbiamo:

14 (t-1) + 4 (t + 2) = 3 (t-1) (t+2)

Eseguendo i calcoli otteniamo:

14t – 14 + 4t + 8 = 3t² + 3t – 6

da cui, sommando i termini simili:

3t² – 15t = 0

Dividendo tutto per 3 e mettendo in evidenza la t, otteniamo:

t (t-5) = 0

che ci fornisce le due soluzioni

• t ₁ = 0
• t ₂ = 5

Dobbiamo ora andare a sostituire i valori ottenuti nella posizione fatta.

Otteniamo due equazioni

• log ₅ x = t ₁  ovvero           log ₅ x = 0
• log ₅ x  = t ₂  ovvero           log ₅ x = 5

Da cui :

• x = 5⁰ = 1
• x = 5⁵

Possiamo accettarle? si , perché entrambe appartengono al C.E.