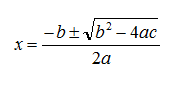DISEQUAZIONI LOGARITMICHE con base a > 1

DISEQUAZIONI LOGARITMICHE con base a > 1

Completiamo l’argomento logaritmi parlando delle disequazioni. 

DISEQUAZIONI LOGARITMICHE con base a > 1. Che cosa si intende con disequazione?

Caro Nipote, ti ricordo che con il termine “disequazione”, in matematica si indica un’espressione in cui, invece del segno di uguaglianza, compare quello di > (maggiore), ≥ (maggiore o uguale), < (minore) , ≤ (minore o uguale).

DISEQUAZIONI Significa diseguaglianze	>	MAGGIORE DI
	≥	MAGGIORE o UGUALE di
	<	MINORE di
	≤	MINORE O UGUALE di

Risolvere una disequazione significa trovare gli intervalli dei valori che, sostituiti alla x, rendono VERA LA DISUGUAGLIANZA

Torneremo poi sull’argomento per un ripasso veloce. Adesso occupiamoci delle DISEQUAZIONI LOGARITMICHE e vediamo che cosa sono e come si risolvono.

DISEQUAZIONI LOGARITMICHE con base a > 1. Che cosa sono le disequazioni

Si dicono disequazioni logaritmiche quelle disuguaglianze in cui l’incognita x compare nell’argomento di uno o più logaritmi.

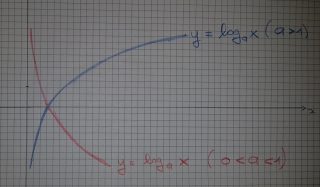
Per poterle risolvere, dobbiamo ricondurci al grafico della funzione logaritmica e ricordarci che abbiamo due grafici distinti, a seconda che la base sia > 1 oppure sia compresa fra 0 ed 1.

Oggi ci occuperemo solo della risoluzione delle disequazioni in caso a>1

DISEQUAZIONI LOGARITMICHE CON a › 1

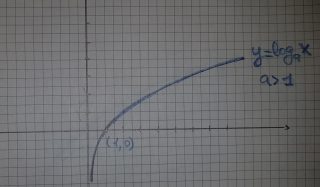
Quando a > 1 la curva logaritmica è crescente e la risoluzione è semplice.

Vediamo insieme come dobbiamo procedere.

1) Innanzitutto impostiamo le condizioni di esistenza:

argomento > 0

In questo modo determiniamo l’intervallo di validità delle soluzioni

2) Cerchiamo di ricondurre la disequazione assegnata in una delle seguenti forme:

log _a f(x) > 0

log _a f(x) < 0

Osserviamo il grafico

Notiamo che 

A)   log _a f(x) > 0 è verificata se

 f(x) > 1 (il logaritmo è positivo se l’argomento è maggiore di 1)

B)   log _a f(x) < 0 è verificata se

0 < f(x) < 1 (il logaritmo è negativo se l’argomento è compreso tra 0 e 1) che equivale a risolvere :

• • f(x) > 0
  • f(x) < 1

Troviamo quindi le soluzioni di A) o di B) e verifichiamo che appartengano all’intervallo di validità.

Facciamo qualche esempio.

DISEQUAZIONI LOGARITMICHE con base a > 1 : esempi

⇒ ESEMPIO 1

Prendiamo la disequazione logaritmica

log₂ x > 1 – log₂ (x-1)

La base è a= 2 > 1, per cui possiamo procedere seguendo lo schema visto sopra.

Innanzitutto impostiamo le condizioni di esistenza. Devono essere gli argomenti del log maggiori di zero:

• x>0
• x- 1 >0

da cui

• x>0
• x > 1

che mi dà : x > 1  ⇔ x∈(1; +∞)

La disequazione assegnata diventa 

log₂ x – 1 + log₂ (x-1) > 0

Siccome 1 = log₂ 2

possiamo scrivere: 

log₂ x – log₂ 2 + log₂ (x-1) > 0

Per le proprietà dei logaritmi, abbiamo

log₂ ((x (x-1)/2) >0

che mi dà 

x (x-1) / 2> 1

Svolgendo i calcoli abbiamo

x (x-1) > 2

x² – x – 2 > 0

A questo punto, dobbiamo determinare le radici dell’equazione di secondo grado corrispondente. Applicando la formula  : 

otteniamo: 

x _1,2 = (1 ± √(1+8))/ 2 = (1 ± 3) / 2

ovvero 

• x₁=2
• x₂ = -1

La disequazione data è soddisfatta per valori esterni all’intervallo delle radici:

x< – 1 ∨ x> 2

Verifichiamo che le soluzioni appartengono all’intervallo di validità. L’unica accettabile è x> 2

⇒ ESEMPIO 2

log x – log 3 <  log (x+2)

Quando la base non è indicata, si intende  a= 10 > 1, per cui possiamo procedere seguendo lo schema visto sopra.

Innanzitutto impostiamo le condizioni di esistenza. Devono essere gli argomenti del log maggiori di zero:

• x>0
• x+ 2 >0

da cui

• x> 0
• x > -2

che mi dà : x > 0   ⇔ x∈(0 ; +∞)

La disequazione assegnata diventa 

log x – log 3 – log (x+2) < 0

che è quindi del secondo tipo. Dobbiamo trovare le soluzioni per cui

0 < f(x) < 1

Per le proprietà dei logaritmi abbiamo

log (x/ 3(x + 2)) < 0

Ovvero

x/ 3(x + 2) < 1

Svolgendo i calcoli abbiamo

• x – 3 (x + 2) < 0
• x – 3x – 6 < 0
• -2x – 6 <0
• 2x + 6 > 0
• x + 3 >0
• x > – 3

Incrociando il risultato ottenuto con l’intervallo di validità, otteniamo che l’unica accettabile è

x > 0

⇒ ESEMPIO 3

 log₃ (x + 1) + log₃ x < log₃ (5x − 3) 

Anche in questo caso a=3 > 0 

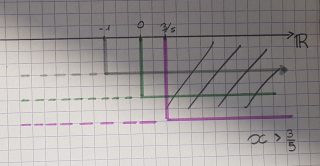
impostiamo le condizioni di esistenza. Devono essere gli argomenti del log maggiori di zero:

• x + 1 > 0
• x > 0
• 5x – 3 > 0

Da cui

• x> – 1
• x> 0
• x > 3/5

ovvero x > 3/5

Risolvendo otteniamo

log ₃ (x + 1) + log ₃ x – log ₃ (5x − 3)  <0

Per le proprietà dei logaritmi

log ₃ (x(x + 1)/(5x-3)) <0

da cui

x(x + 1)/(5x-3) < 3⁰

Siccome 3⁰ = 1

possiamo scrivere

x(x + 1)/(5x-3) < 1

ovvero:

x(x + 1) < 5x-3

Svolgendo i calcoli, abbiamo

x² + x – 5x + 3 < 0

a cui corrisponde l’equazione di secondo grado

x² – 4x + 3 = 0

Applicando la formula  : 

otteniamo: 

x _1,2 = (4 ± √(16+12))/ 2 = (4 ± 2) / 2

• x₁= 1
• _x2= 3

Tale disequazione è negativa per valori compresi all’interno dell’intervallo delle radici

Siccome 1 > 3/5, le soluzioni sono 1<x<3

Nel prossimo articolo ci occuperemo delle disequazioni logaritmiche con  0 < a < 1