DISEQUAZIONI LOGARITMICHE con base 0< a < 1

DISEQUAZIONI LOGARITMICHE con base 0< a < 1

Dopo le disequazioni con base > 1, occupiamoci adesso di quelle con base compresa tra 0 e 1.

Ricordate:

Si dicono disequazioni logaritmiche quelle disuguaglianze in cui l’incognita x compare nell’argomento di uno o più logaritmi.

Come abbiamo visto anche nel caso precedente, per risolvere queste disequazioni dobbiamo ricondurci al grafico della funzione logaritmica, ricordando che, nel caso la base sia compresa tra 0 e 1, la funzione logaritmica è una funzione decrescente in R⁺. Ovvero: la y diminuisce all’aumentare di x.

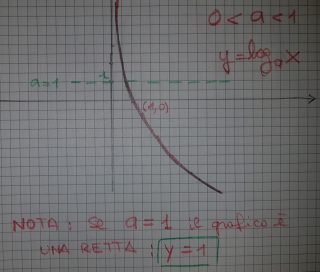
Dal grafico vediamo che la funzione y = log _a x , con 0< a <1 gode delle seguenti proprietà

• è definita solo per x > 0 (ovvero ha come dominio R ⁺ e come codominio R
• è monotona decrescente
• incontra gli assi in (1, 0)
• è positiva per 0< x <1
• diventa negativa per x>1

DISEQUAZIONI LOGARITMICHE CON a › 1

Quando 0 < a < 1 la curva logaritmica è decrescente. Anche in questo caso procediamo come segue. 

1) Innanzitutto impostiamo le condizioni di esistenza:

argomento > 0

In questo modo determiniamo l’intervallo di validità delle soluzioni

2) Cerchiamo di ricondurre la disequazione assegnata in una delle seguenti forme:

log _a f(x) > 0

log _a f(x) < 0

Osserviamo il grafico

Notiamo che

(A)   log _a f(x) > 0

poiché il logaritmo assume valori positivi per valori dell’argomento compresi tra 0 e 1, la condizione da porre sarà:

0 < f(x) < 1 (il logaritmo è positivo se l’argomento è compreso tra 0 e 1)

ovvero dobbiamo risolvere il sistema :

• • f(x) > 0
  • f(x) < 1

(B)   log _a f(x) < 0

In questo caso, siccome il logaritmo assume valori negativi per valori dell’argomento maggiori di 1, la condizione da porre sarà

 f(x) > 1 (il logaritmo è negativo se l’argomento è maggiore di 1)

Dopo aver trovato le condizioni di accettabilità, andiamo a risolvere le disequazioni assegnate e verifichiamo che esse appartengano all’intervallo di validità.

Facciamo qualche esempio.

DISEQUAZIONI LOGARITMICHE con base 0< a < 1. Esempi svolti

⇒ ESEMPIO 1

log_{1 /3}  (3-x) > log _{1 /3} (2x + 6)

siccome a = 1/3 < 1, siamo naturalmente nel caso in esame.

Seguiamo il procedimento che ti ho illustrato sopra e cominciamo impostando le condizioni di esistenza del log:

• 3-x> 0
• 2x + 6 > 0

Risolvendo otteniamo

• x< 3
• x > – 3

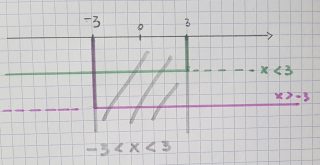
Siccome è un sistema di disequazioni, l’intervallo di validità coincide con quello in cui sono soddisfatte entrambe le disequazioni (ovvero sul grafico dobbiamo vedere solo linee continue sovrapposte).

In questo caso abbiamo

-3 < x < 3

Ci riportiamo a una delle due forme viste sopra utilizzando le proprietà dei log.

Si riconduce la disequazione assegnata ad una delle due forme presenti in (1) utilizzando le proprietà dei logaritmi

log_{1 /3}  (3-x) – log _{1 /3} (2x + 6) > 0

log_{1 /3}  ((3-x)/(2x + 6)) > 0

dobbiamo imporre che l’argomento sia compreso tra 0 e 1:

• 3-x/(2x + 6) >0
• 3-x/(2x + 6) < 1

Ovvero

• 3-x > 0
• 3-x < 2x + 6

Da cui

• x<3
• x> – 1

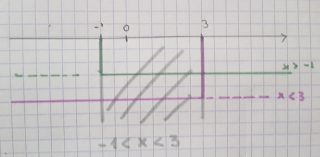La soluzione è data da tutte le x ∈(-1; 3)

Verifichiamo ora che le soluzioni appartengano all’intervallo di validità.

Siccome  (-1; 3) è contenuto in (-3 ; 3 ), le soluzioni sono accettabili.

⇒ ESEMPIO 2

Si consideri la disequazione logaritmica

log _{1 /2} (x + 1) + log_{1 /2} (6x − 2) − log _{1 /2}  (5x + 1) > log_{1 /2}  4

siccome a = 1/2 < 1

siamo nuovamente nel caso in esame.

Impostiamo le condizioni di esistenza del log:

• x+ 1 > 0
• 6x – 2 > 0
• 5x + 1 > 0

Ovvero

• x > – 1
• x > 1/3
• x > -1/5

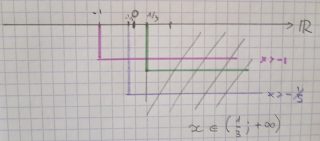
Siccome è un sistema di disequazioni, l’intervallo di validità coincide con quello in cui sono soddisfatte tutte le disequazioni (ovvero sul grafico dobbiamo vedere solo linee continue sovrapposte). In questo caso abbiamo

x ∈(1/3; +∞)

Riportiamoci ora  a una delle due forme viste sopra utilizzando le proprietà dei log.

In questo caso:

log _{1 /2} (x + 1) + log_{1 /2}   (6x − 2) − log _{1 /2}  (5x + 1) > log_{1 /2}  4

log _{1 /2}{[ (x + 1) (6x – 2)/ 4 (5x +1)] } > 0

Anche in questo secondo esempio, dobbiamo imporre che l’argomento sia compreso tra 0 e 1:

• (x + 1) (6x – 2)/ 4 (5x +1) >0
• (x + 1) (6x – 2)/ 4 (5x +1) < 1

Risolvendo otteniamo

• (x + 1) (6x – 2) > 0
• (x + 1) (6x – 2)< 4 (5x +1)

Da cui

• x₁> – 1 ∨ x₂ > 1/3
• 6x² + 4x – 2 < 20x + 4 ⇒ 6x² + 16x – 6 < 0 ⇒ risolvendo l’equazione di secondo grado associata abbiamo x₃= 3 ∨ x₄ = 1/3. La disequazione è negativa per valori interni all’intervallo (1/3; 3).

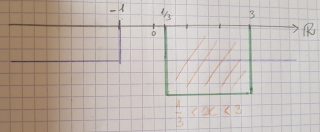
Anche stavolta, il sistema è soddisfatto solo dove le “soluzioni si sovrappongono”:

Abbiamo quindi l’intervallo (1/3; 3), che appartiene all’intervallo di accettabilità.

La soluzione è data da tutte le x ∈(1/3; 3)